
Ingenieurbüro für angewandte Strömungsmechanik
Kontakt+ Wir über uns
+ Neuheiten
+ Veranstaltungen
+ Anwendungsbeispiele
- Technische Hintergrunde
- Kosten und Nutzen: Einführung
- CAD
- Gitter
- Gittersorten
- Gittertopologien
- Gitterqualität eine Kunst
- Alternativen zur Gittergenerierung
- Bewegte Objekte
- Gitterkosten
- Schaumfliesseigenschaften
+ Support
+ Impressum
+ Nutzungsbedingungen
Bewegte Objekte
In vielen Situationen können bewegte Teile die Strömungsbedingungen durch Beschleunigungskräfte und/oder Verdrängung des Fluids maßgeblich beeinflussen. In solchen Fällen müssen die Simulationen solche Bewegungsabläufe berücksichtigen.
Dabei kann hier zwischen zwei Kategorien unterschieden werden:
- Vordefinierbare Bewegungen:
- Sich auf Grund der Strömungskräfte ergebenden Bewegungen
Die Bewegung der Wände oder von Bauteilen innerhalb des Lösungsgebietes sind bekannt. In der Regel handelt es sich hierbei um angetriebene oder gesteuerte Bewegungen. Dazu gehört zum Beispiel die Schaufelbewegung einer angetriebenen Pumpe.
In diesem Fall beschränkt sich die Simulation auf die Integration der Navier-Stokes'schen-Gleichungen. Die damit verbundenen wirtschaftlichen Aspekte umfassen die sich ergebenden Rechenzeiten und die Definition eines stabilen Gitters oder von Gitterbestandteilen, die eine Verzerrung der Zellen vermeiden.
Viele Bewegungsabläufe ergeben sich aus der Bilanzierung vieler wirkender Kräfte, wie zum Beispiel die Bewegungen eines Segels.
In diesem Fall kommen zusätzlich zu der oben beschriebenen Simulationsaufwendungen die Beschreibung der Mechanik und ggf. die Spannungen innerhalb des Festkörpers. Man spricht daher in diesem Fall von gekoppelten Systemen (CFD-Mechanik-Strukturanalyse) oder von Multi-Physik-Anwendungen. Ein Beispiel einer gekoppelten Simulation (Strömung+Mechanik) finden Sie hier.
Im Folgenden werden die unterschiedlichen Methoden diskutiert, die bei der Abbildung von Bewegungsabläufen angewandt werden.
Bewegte KoordinatensystemeBewegt sich das ganze Lösungsgebiet, dann kann ein bewegtes Koordinatensystem definiert werden. Dabei werden in jeder Berechnungszelle die Beschleunigungskräfte als vorgegebene Quellterme berücksichtigt. Der Vorteil dabei ist, dass keine zeitliche Betrachtung der Geschehnisse erfolgen muss. Die Strömungsbedingungen können als zeitlich konstant bzw. stationär betrachtet werden. Die Auswirkung auf die Simulationskosten ist sehr positiv. Die Berechung erfolgt stationär mit der Folge, dass die langen Rechenzeiten transienter Berechnungen vermieden werden. Zusätzlich entfällt die Beschreibung der Gitterbewegung im dreidimensionalen Raum. Ein Beispiel dafür ist der Raum in einer rotierenden Trommel. Die Darstellung der Fluidströmung kann entweder relativ zum bewegten Koordinatensystem oder in absoluten Koordinaten erfolgen. Eine einfache Umrechnung zwischen beiden Darstellungsformen ist unter Berücksichtigung des Rotationsradius und der -geschwindigeit machbar und wird in der Regel von den Postprozessoren als Standardoption angeboten. |
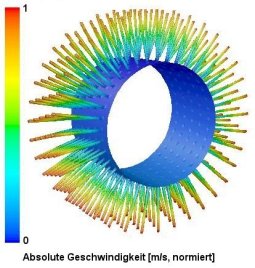 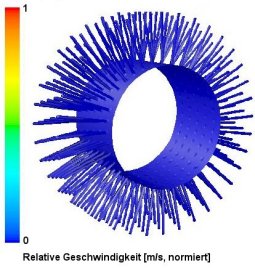 |
Bewegte ObjekteEntsteht eine starke Wechselwirkung zwischen den bewegten und den nicht bewegten Teilen eines Gerätes, dann sollte eine Unterteilung des Lösungsgebietes in einen bewegten und einen nicht bewegten Teil vorgenommen werden. Bewegen sich mehrere Teile unabhängig von einander, ist das Lösungsgebiet in entsprechend viele Teilgebiete zu unterteilen. Die Abbildung der Bewegung kann nur durch eine transiente Simulation erfolgen. Das hier gezeigte Beispiel zeigt ein Verbrennungsmotor, bei dem die Kolben-, die Kurbel- und die Kurbelwellenbewegungen berücksichtigt werden. Die Bewegungsabläufe umfassen eine Translation (Kolben) eine Rotation (Kurbelwelle) sowie eine Kombination beider (Kurbelwelle). Einige Techniken, jeweils mit Vor- und Nachteilen, zur Abbildungen von bewegten Teilen stehen zur Verfügung: |
 Bild klicken für Animation (51 kB)
ESC zum Anhalten |
Gleitende Gitter werden oft zur Abbildung von Rührern oder Pumpen angewandt. Sie haben den entscheidenden Vorteil gegenüber rotierenden Koordinatensystemen, dass sie Rotor-Stator-Interaktionen berücksichtigen, d.h. sie bilden zeitlich unterschiedliche Rotor-Stator-Stellungen ab. Bei dieser Technik werden die Verbindungen zwischen den Berechnungszellen bei jedem Zeitschritt neu definiert. Dies erfolgt je nach Programm durch eine Verschiebung und Verzerrung der Gitterlinien, durch eine neue Zuordnung der Knoten oder durch eine Interface-Lage, die zwischen beiden Gitterteilen interpoliert. Im Gegensatz zu den rotierenden Koordinatensystemen müssen gleitende Gitter transient berechnet werden. Gleitende Gitter haben den Vorteil, dass sie bei gut beschreibbaren Bewegungsbahnen, wie einer Rotation oder einer Translation, relativ einfach aufgebaut werden können. Je komplizierter die Bewegung desto schwieriger wird der Gitteraufbau. |
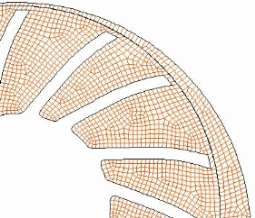 Bild klicken für Animation (1309 kB)
ESC zum Anhalten |
Die Veränderung der Position oder der Form eines Objektes kann durch eine Deformation der Gitterlinien beschrieben werden. Die Knoten können mit der benötigten Bewegungsgeschwindigkeit verschoben werden und somit wird das gesamte Gitter zur Abbildung der Bewegungsabläufe verändert. Dabei ist zu berücksichtigen, dass der Raum und das Volumen konserviert werden müssen - d.h. die Strömungsimpulse dürfen nicht durch die Bewegung von Gitterlinien verfälscht werden. Die numerischen Hintergründe sind etwas komplizierter als bei bewegten Koordinaten oder bei gleitenden Gittern. Dies ist jedoch für die Anwender weniger relevant, da viele Programme diese Funktionalität beinhalten. Das Hauptproblem liegt in der, während der Verschiebung der Knoten entstehenden, Verzerrung der Rechenzellen. Bei starken Deformationen oder bei komplexen Bewegungsbahnen kann die damit verbundene Gitterverzerrung zu ernsthaften Kovergenzproblemen führen. Sollte sich dabei noch die Gitterbewegung sich auf Basis von errechneten Drücke und Spannung ergeben, kann am Anfang der Gitterbeschreibung schwer abgeschätzt werden, wie die Gittertopologie zu gestalten ist. In dem hier dargestellten Beispiel wird die Deformation einer Gummilippe in Folge von schwankenden Druckkräften berechnet. Die Deformation ist relativ klein und lässt sich mit Hilfe eines bewegten unstrukturierten Gitters darstellen. Wird anstelle von diesem Material ein weicheres Material angewandt, sind große Deformationen zu erwarten, die den Einsatz dieser Technik verhindert. |
 Bild klicken für Animation (51 kB)
ESC zum Anhalten
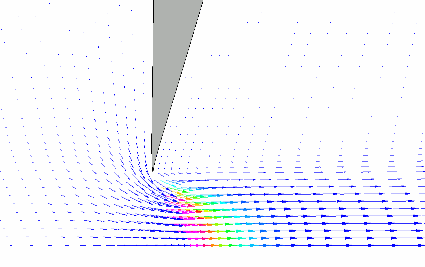 Bild klicken für Animation (282 kB)
ESC zum Anhalten |
Bei diesem Verfahren werden CAD-Modelle zur Abbildung der unterschiedlichen Objekte in einem kartesischen Koordinatensystem eingelesen. Die Bewegungsbahn, die Geschwindigkeiten und die Beschleunigung der bewegten Objekte werden jeweils definiert. Am Anfang jedes Zeitschrittes berechnet das Programm die neue Position der unterschiedlichen Objekte und berechnet dann die Schnittflächen aller Zellen. Somit wird der durchströmte Raum immer wieder aktualisiert. Eine Erhaltung des Raumes und der Volumina wird berücksichtigt, damit die Fluidverdrängung korrekt abgebildet wird. Das Prinzip der automatischen Geometrieerkennung wird hier ausführlicher beschrieben. Diese Methode verspricht eine radikale Minderung der Gitterkosten und bietet wesentliche Vorteile gegenüber den oben beschriebenen Methoden der Gittermanipulation. Bei Grenzanwendungungen, wie etwa ein Rührer, kann sowohl ein gleitendes Gitter als auch die dynamische Teilzellenblockierung gleich effizient eingesetzt werden. In den Fällen jedoch wo viele Bauteile komplexe Bewegungsabläufe aufweisen, sind Gittermanipulationsmethoden durch drohende Zellverzerrungen doch stark eingeschränkt. Der Nachteil dieser Methode liegt in der Anwendung von kartesischen Gittern, die zwar eine ideale Grundlage für die Numerik anbieten führen aber in der Regel zu sehr großen Gitterdimensionen und somit zu hohen Speicher- und Rechenzeitansprüchen führen. Das hier dargestellte Beispiel eines rollenden Vierecks verdeutlicht die Probleme, die bei einer Gittermanipulation auftreten würden. Weitere Beispiele zeigen mehrphasige Berechnungen zur Bestimmung der Oberflächendeformation und die Geschwindigkeitsverteilung mehrerer Fluide. |
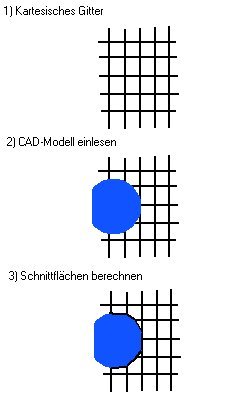
 Bild klicken für Animation (150 kB)
ESC zum Anhalten  Bild klicken für Animation (223 kB)
ESC zum Anhalten 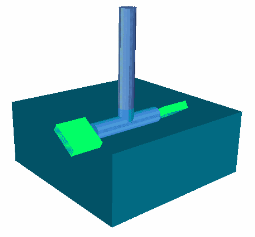 Bild klicken für Animation (50 kB)
ESC zum Anhalten  Bild klicken für Animation (77 kB)
ESC zum Anhalten |